一、Shor算法概述
Shor算法是由Peter Shor于1994年提出的一种量子计算算法,能够在多项式时间内对大整数进行质因数分解。这一算法的诞生彻底改变了密码学界对安全性的认知——它可直接破解RSA、ECC等现代公钥密码体系的基础数学难题。在量子计算机上运行Shor算法,可将原本需要指数级时间的大整数分解问题转化为多项式时间问题,对依赖数论难题的加密体系构成根本性威胁。
二、技术原理深度解析
1. 数学基础:从难题到可解
Shor算法的核心在于将质因数分解问题转化为周期查找问题,利用量子计算的并行性高效求解周期:
关键步骤:
- 随机选择整数 $a$($1 < a < N$)
- 计算 $f(x) = a^x \mod N$ 的周期 $r$
- 若 $r$ 为偶数且 $a^{r/2} \not\equiv -1 \mod N$,则:
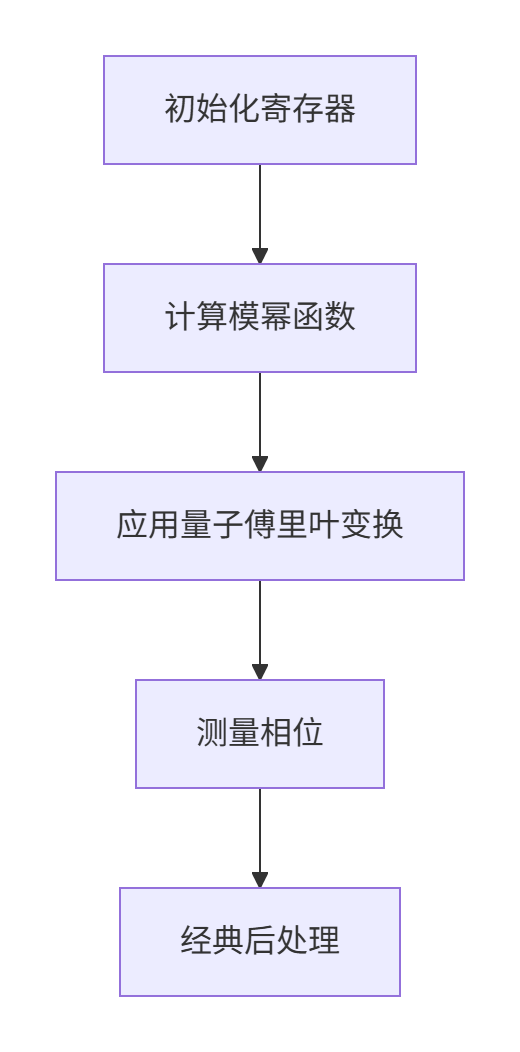
2. 量子电路设计
Shor算法的量子部分包含两个核心模块:
(1)量子傅里叶变换(QFT)
(2)周期查找电路
3. 复杂度对比
| 算法类型 | 时间复杂度 | 空间复杂度 |
|---|---|---|
| 经典算法(试除法) | $O(\sqrt{N})$ | $O(1)$ |
| 经典算法(数域筛法) | $e^{(64/9)^{1/3}(\log N)^{1/3}(\log \log N)^{2/3}}$ | $O(\log N)$ |
| Shor算法 | $O((\log N)^3)$ | $O(\log N)$ |
三、应用场景分析
1. 密码学领域冲击
| 加密体系 | 受影响程度 | 破解时间预估(量子计算机) |
|---|---|---|
| RSA-2048 | 完全破解 | 数小时(100万量子比特) |
| ECC-256 | 完全破解 | 分钟级(2000逻辑量子比特) |
| DH密钥交换 | 完全破解 | 与RSA相当 |
2. 实际攻击场景模拟
(1)金融系统攻击链
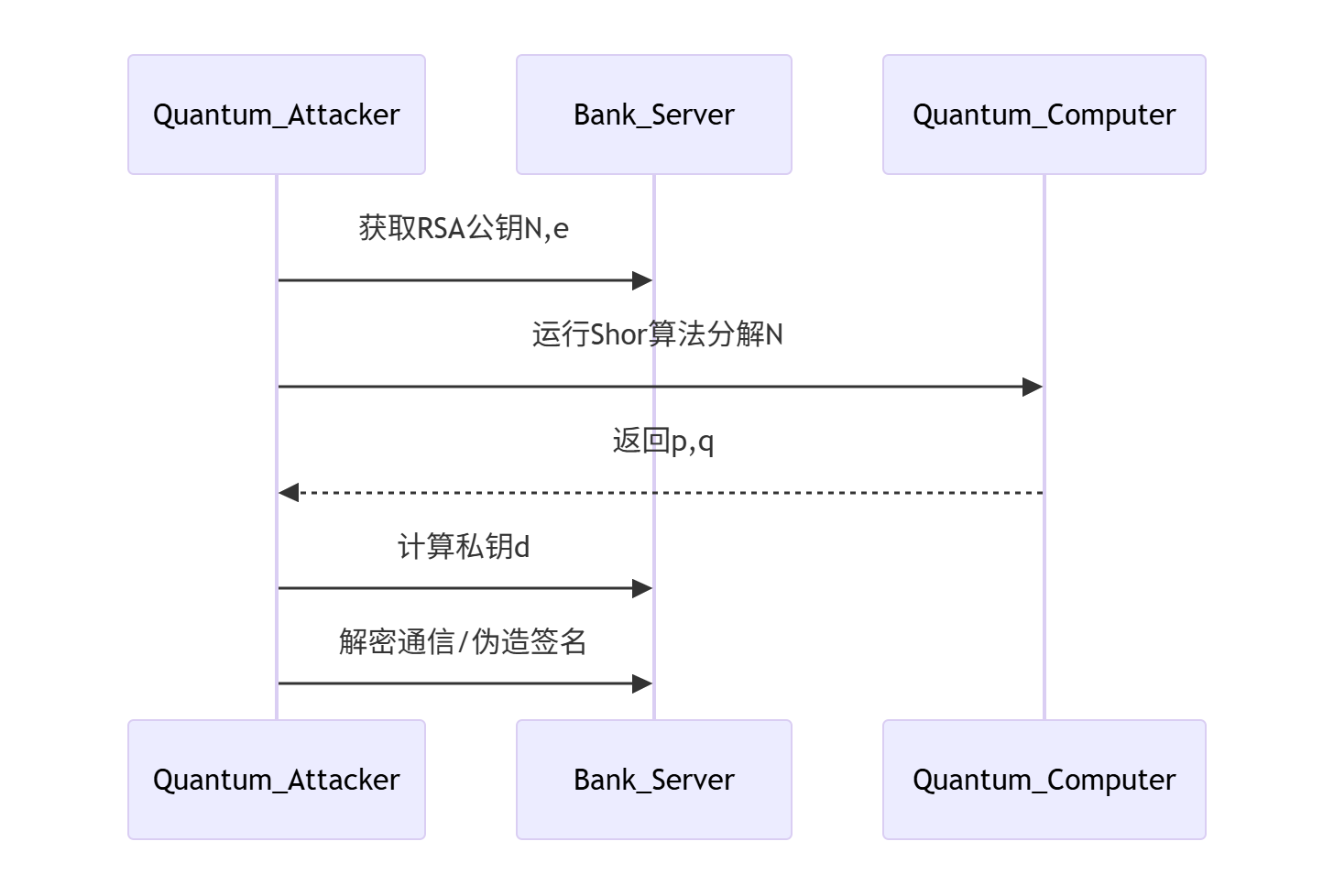
(2)区块链安全威胁
- 比特币:椭圆曲线数字签名算法(ECDSA)被破解
- 以太坊:账户私钥可被批量恢复
- 跨链协议:密钥交换机制失效
四、优缺点对比分析
1. 核心优势
- 指数级加速:将大整数分解从不可行变为可行
- 数学普适性:可扩展至其他周期查找问题
- 理论完备性:已被严格数学证明
2. 现存局限性
| 挑战类型 | 具体问题 | 当前解决方案 |
|---|---|---|
| 量子硬件 | 需要百万级物理量子比特 | 逻辑量子比特纠错编码 |
| 错误纠正 | 表面码需1000:1冗余 | 量子纠错码优化 |
| 经典预处理 | 随机数生成与验证 | 改进随机数筛选算法 |
五、代码示例与实验模拟
1. 经典模拟Shor算法(Python)
1 | import math |
注意:此代码仅为演示算法逻辑,实际量子实现需用量子电路。
2. Qiskit量子实现框架
1 | from qiskit import QuantumCircuit, Aer, execute |
六、未来发展趋势
1. 量子硬件突破路线图
| 年份 | 里程碑 | 技术指标 |
|---|---|---|
| 2025 | 逻辑量子比特演示 | 100-1000个纠错逻辑比特 |
| 2030 | 商用密码破解原型 | 百万物理量子比特 |
| 2035 | 全面密码威胁 | 实用化Shor算法实现 |
2. 抗量子密码学应对
- NIST PQC标准:CRYSTALS-Kyber(密钥交换)、Dilithium(签名)
- 混合加密模式:RSA+Kyber双轨并行
- 量子随机数生成:增强密钥不可预测性
3. 新兴应用领域
- 量子区块链:抗量子签名方案
- 太空通信安全:量子安全密钥分发
- 基因组隐私保护:长期数据加密
七、防御策略与应对建议
1. 过渡期防护措施
- 密钥长度升级:RSA-4096、ECC-521
- 算法替换计划:逐步迁移至PQC标准
- 量子安全评估:定期进行密码体系审计
2. 长期战略规划
1 | gantt |
Shor算法的出现标志着密码学进入”量子时代”。尽管实用化量子计算机仍面临技术挑战,但密码学界已开始积极应对。理解Shor算法的原理与影响,不仅是技术人员的必修课,更是守护数字世界安全的战略需要。在量子计算与抗量子密码学的博弈中,主动布局、提前防御将成为决定未来网络安全格局的关键因素。







