一、Diffie-Hellman算法概述
Diffie-Hellman(迪菲-赫尔曼)算法是密码学史上第一个公开的密钥交换协议,由Whitfield Diffie和Martin Hellman于1976年提出。这项革命性发明解决了在不安全信道上安全交换密钥的难题,为现代密码学奠定了基础。如今,Diffie-Hellman算法及其衍生方案(如ECDH)已成为TLS/SSL、IPSec、SSH等关键网络协议的核心组件,支撑着互联网80%以上的安全通信。
二、Diffie-Hellman算法原理深度解析
1. 数学基础:离散对数问题
算法的安全性基于有限域上的离散对数问题:
- 给定一个大素数p和其原根g,计算 $g^x \mod p$ 是容易的
- 但已知 $g^x \mod p$ 和 $g^y \mod p$,求 $x$ 或 $y$ 在计算上是不可行的
2. 密钥交换流程
(1)参数协商阶段
通信双方预先约定:
- 大素数p(模数)
- 原根g(生成元)
(2)密钥生成与交换
1 | # Alice端计算 |
(3)数学推导
3. 安全性分析
- 前向保密:即使长期私钥泄露,历史会话密钥仍安全
- 抵抗被动攻击:窃听者只能获取 $g^x \mod p$ 和 $g^y \mod p$,无法计算共享密钥
- 中间人攻击风险:需配合数字签名或证书验证身份
三、Diffie-Hellman算法的应用场景
1. 安全通信协议
| 协议 | 应用场景 | 实现方式 |
|---|---|---|
| TLS/SSL | HTTPS加密 | DHE_RSA、ECDHE_ECDSA |
| IPSec | VPN隧道 | IKEv1/IKEv2密钥交换 |
| SSH | 安全远程登录 | Diffie-Hellman Group Exchange |
2. 区块链与加密货币
- 比特币:椭圆曲线Diffie-Hellman(ECDH)用于钱包间密钥协商
- 以太坊:P2P网络节点身份验证
- 零知识证明:zk-SNARKs中的密钥生成
3. 物联网安全
1 | // 嵌入式设备中的ECDH实现示例 |
四、Diffie-Hellman算法的变种与优化
1. 传统DH vs ECDH对比
| 特性 | 传统DH | 椭圆曲线DH (ECDH) |
|---|---|---|
| 密钥长度 | 2048位 | 256位 |
| 计算效率 | 较慢 | 快10倍以上 |
| 带宽消耗 | 高 | 低 |
| 标准化 | RFC 3526 | RFC 7748 |
2. 现代实现方案
(1)临时DH(DHE)
- 每次会话生成临时密钥对
- 提供前向保密性
(2)椭圆曲线DH(ECDH)
- 基于椭圆曲线密码学
- 更短的密钥提供同等安全性
(3)混合加密方案
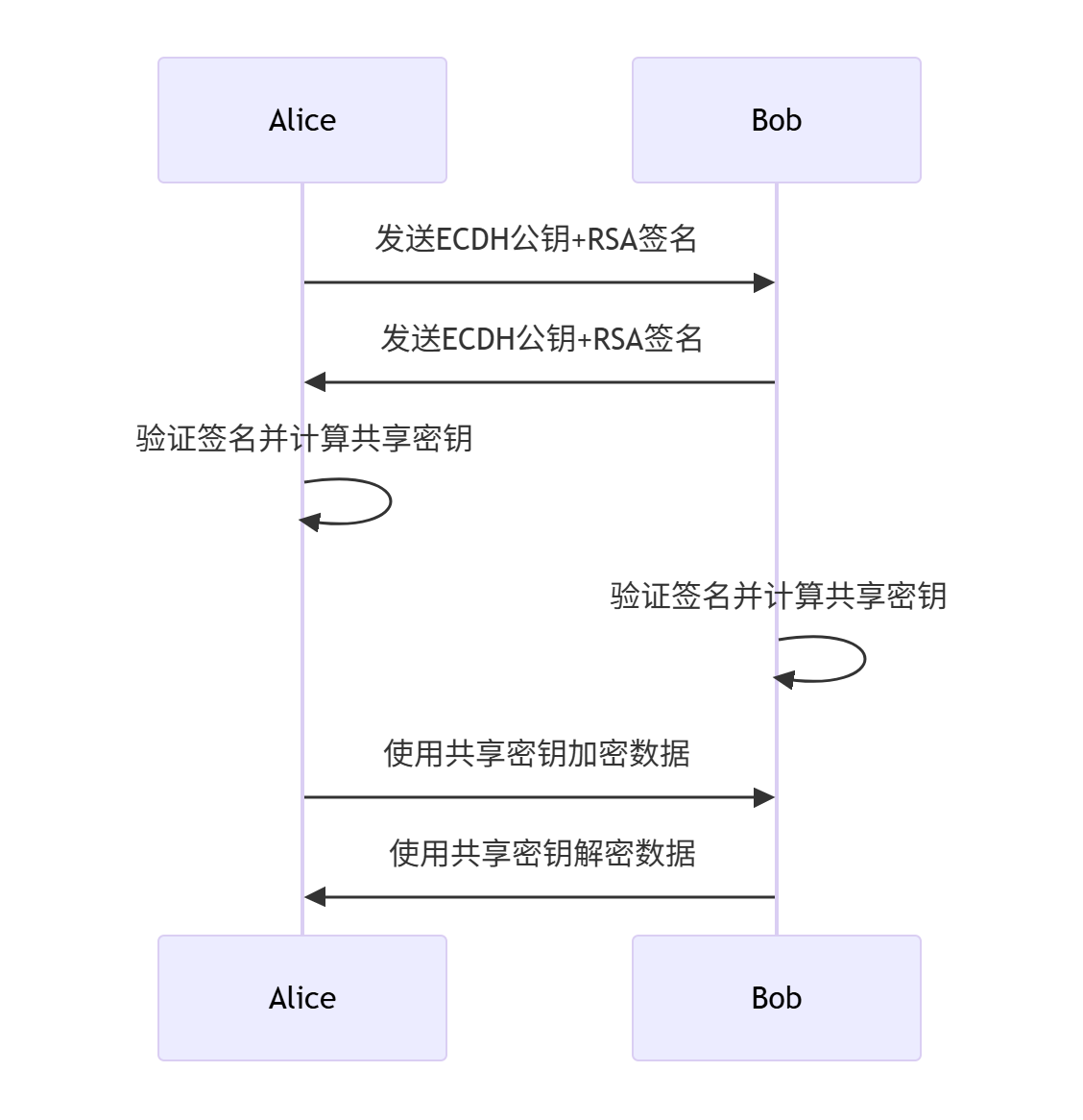
五、Diffie-Hellman算法的优缺点分析
1. 核心优势
- 密钥交换革命:首次实现不安全信道上的安全密钥协商
- 前向保密保障:临时密钥机制防止历史会话泄露
- 计算效率高:相比RSA密钥交换更节省资源
- 标准化支持:广泛兼容现有网络协议栈
2. 现存局限性
- 中间人攻击风险:需配合身份认证机制
- 参数选择敏感:弱素数可能导致破解(如Logjam攻击)
- 量子计算威胁:Shor算法可高效解决离散对数问题
3. 安全增强措施
- 使用大素数:RFC 3526定义的2048/3072/4096位素数
- 前向保密配置:禁用静态DH,强制使用DHE/ECDHE
- 证书绑定:将DH公钥与数字证书绑定验证
六、代码示例:完整DH密钥交换实现
1 | from cryptography.hazmat.primitives import serialization |
七、未来发展趋势
后量子密码学替代方案
- 基于格的密钥交换(如Kyber算法)
- NIST后量子密码标准化进程
协议优化方向
- 硬件加速的椭圆曲线运算
- 批处理密钥交换协议
新型应用场景
- 量子互联网中的密钥分发
- 元宇宙虚拟世界身份认证
标准化演进
- TLS 1.3强制使用ECDHE
- IPSec/IKEv2的现代加密套件
Diffie-Hellman算法作为密码学基石,其数学优雅性与工程实用性持续影响着现代通信安全。尽管面临量子计算的潜在威胁,通过与其他技术的创新结合(如混合加密、后量子密码),DH类算法仍将在可预见的未来继续守护数字世界的安全通信。对于开发者而言,深入理解DH原理不仅有助于构建安全的系统,更是应对未来密码学挑战的重要基础。








