量子行走：量子计算的超强搜索算法

一、量子行走概述

量子行走（Quantum Walk）是经典随机行走在量子力学框架下的扩展，通过叠加态和干涉效应实现信息处理的高效算法。作为量子计算领域的核心算法之一，量子行走在搜索、图论、优化等问题上展现出超越经典算法的指数级加速潜力。自2001年Ahlswede等人提出连续时间量子行走、2003年Childs等人提出离散时间量子行走以来，该技术已成为量子算法设计的重要工具，尤其在未排序数据库搜索、图同构判断等领域具有颠覆性应用前景。

---

二、技术原理深度解析

1. 经典 vs 量子行走对比

特性	经典随机行走	量子行走
状态空间	离散位置节点	位置-硬币态联合系统
转移规则	概率转移矩阵	酉演化算子
干涉效应	无	相位叠加与干涉
搜索效率	$O(N)$	$O(\sqrt{N})$（连续时间）/$O(\sqrt{N\log N})$（离散时间）

2. 离散时间量子行走核心组件

（1）硬币算子（Coin Operator）

$$C = \begin{pmatrix} \cos\theta & \sin\theta \\ \sin\theta & -\cos\theta \end{pmatrix}$$

作用：在硬币空间制备叠加态

（2）移位算子（Shift Operator）

$$S = \sum_x |x+1\rangle\langle x|\otimes |R\rangle\langle R| + |x-1\rangle\langle x|\otimes |L\rangle\langle L|$$

作用：根据硬币态决定位置移动方向

（3）整体演化

$$U = S \cdot C$$

3. 连续时间量子行走模型

$$H = -\gamma A$$

其中$A$为图的邻接矩阵，$\gamma$为耦合强度，演化算子为：

$$|\psi(t)\rangle = e^{-iHt}|\psi(0)\rangle$$

---

三、应用场景分析

1. 搜索算法优化

（1）未排序数据库搜索

# 量子行走搜索算法伪代码
def quantum_search(database, target):
    # 初始化：均匀叠加态
    psi = uniform_superposition(len(database))
    
    # 定义Oracle：标记目标元素
    oracle = create_oracle(database, target)
    
    # 扩散算子：振幅放大
    diffusion = create_diffusion_operator(len(database))
    
    # 迭代次数：O(sqrt(N))
    iterations = int(pi/4 * sqrt(len(database)))
    
    # 量子行走迭代
    for _ in range(iterations):
        psi = oracle(psi)
        psi = diffusion(psi)
    
    # 测量结果
    return measure(psi)

优势：相比经典搜索$O(N)$，量子行走实现$O(\sqrt{N})$复杂度

2. 图论问题求解

（1）图同构判断

• 通过量子行走在图结构上的演化差异识别同构性
• 相比经典算法指数级加速

（2）最短路径问题

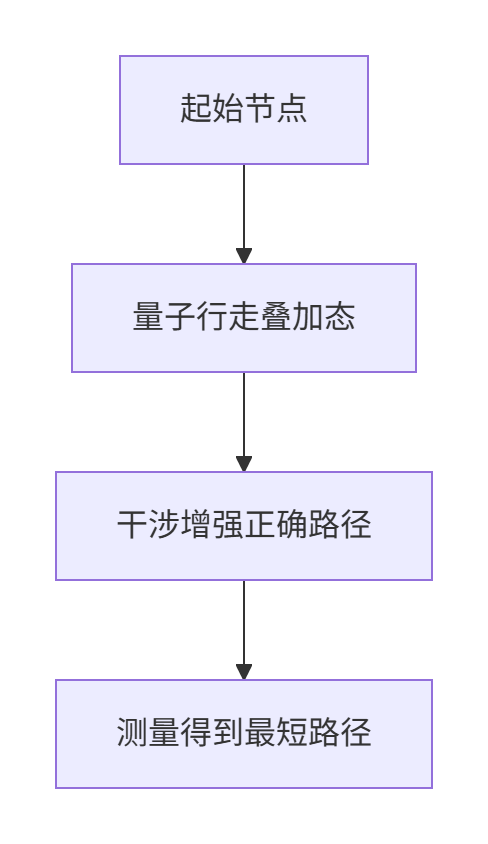
3. 机器学习加速

• 量子支持向量机：通过量子行走优化核函数计算
• 量子聚类算法：利用行走特性加速数据点分类

---

四、优缺点对比分析

1. 核心优势

特性	优势表现
计算速度	搜索问题指数级加速
普适性	适用于多种图结构问题
并行性	叠加态同时探索多路径
可扩展性	适用于高维复杂网络

2. 现存局限性

挑战类型	具体问题	当前解决方案
量子硬件	需要大量量子比特	表面码纠错编码
退相干问题	量子态易受干扰	动态纠错技术
算法设计	复杂问题需定制行走规则	通用框架开发

---

五、代码示例与实验模拟

1. 离散时间量子行走模拟（Python）

import numpy as np
from math import pi, cos, sin

def quantum_walk_simulation(steps, coin_angle=pi/4):
    # 初始化系统状态 (位置|0> + 位置|1>) / sqrt(2)
    psi = np.array([1/np.sqrt(2), 0, 0, 1/np.sqrt(2)])  # |0L>, |0R>, |1L>, |1R>
    
    # 定义硬币算子 (Hadamard-like)
    theta = coin_angle
    C = np.array([[cos(theta), sin(theta)],
                  [sin(theta), -cos(theta)]])
    
    # 定义移位算子
    S = np.array([[1, 0, 0, 0],
                  [0, 0, 1, 0],
                  [0, 1, 0, 0],
                  [0, 0, 0, 1]])
    
    # 演化算子
    U = S @ C.reshape(2,2)  # 简化版本
    
    # 执行量子行走
    for _ in range(steps):
        psi = U @ psi
    
    # 测量位置概率
    prob_0 = np.abs(psi[0])**2 + np.abs(psi[1])**2
    prob_1 = np.abs(psi[2])**2 + np.abs(psi[3])**2
    
    return prob_0, prob_1

# 示例：执行10步量子行走
print(quantum_walk_simulation(10))

2. 连续时间量子行走模拟（Qiskit框架）

from qiskit import QuantumCircuit, Aer, execute
from qiskit.circuit.library import RYGate

def continuous_quantum_walk(n_qubits=3, gamma=0.1):
    qc = QuantumCircuit(n_qubits)
    
    # 初始状态制备 (|000> + |001> + ... + |111>) / sqrt(8)
    qc.h(range(n_qubits))
    
    # 模拟邻接矩阵作用 (简化版)
    for i in range(n_qubits):
        for j in range(i+1, n_qubits):
            # 添加控制相位门模拟图连接
            if abs(i-j) == 1:  # 相邻节点连接
                qc.cp(gamma, i, j)
    
    # 时间演化算子 (简化)
    qc.rz(2*gamma, range(n_qubits))
    
    # 测量
    qc.measure_all()
    
    # 模拟运行
    backend = Aer.get_backend('qasm_simulator')
    result = execute(qc, backend, shots=1000).result()
    counts = result.get_counts()
    
    return counts

# 示例：3量子比特连续时间行走
print(continuous_quantum_walk())

---

六、未来发展趋势

1. 硬件实现路线图

年份	技术节点	目标规模
2025	100-1000物理量子比特	小规模图问题求解
2030	逻辑量子比特纠错	中等规模网络分析
2035	百万物理量子比特	复杂系统模拟

2. 新兴应用领域

• 量子化学：分子轨道演化模拟
• 金融网络：风险传播路径预测
• 生物系统：蛋白质折叠路径优化

3. 混合计算架构

---

七、防御策略与应对建议

1. 算法优化方向

• 动态硬币算子：自适应调整演化规则
• 多维行走：扩展至高维图结构
• 混合算法：结合经典启发式方法

2. 技术发展建议

gantt
    title 量子行走研发计划
    section 基础研究
    理论模型优化       :20XX, 12m
    复杂度证明         :20XX, 6m
    section 应用开发
    图算法实现         :20XX, 18m
    机器学习集成       :20XX, 12m
    section 硬件适配
    量子芯片设计       :20XX, 24m
    误差校正方案       :20XX, 12m

量子行走作为量子计算的超强算法引擎，正在重新定义信息处理的边界。尽管面临硬件实现和算法设计的多重挑战，其在搜索、图论等领域的指数级加速潜力已得到理论验证。随着量子硬件技术的进步和算法优化，量子行走有望在药物研发、金融分析、网络安全等领域率先实现实用化突破。对于科研人员和工程师而言，掌握量子行走的数学原理和工程实现方法，将成为抢占未来技术制高点的关键竞争力。