堆(Heap)是一种特殊的树形数据结构,它满足以下性质(堆序性):
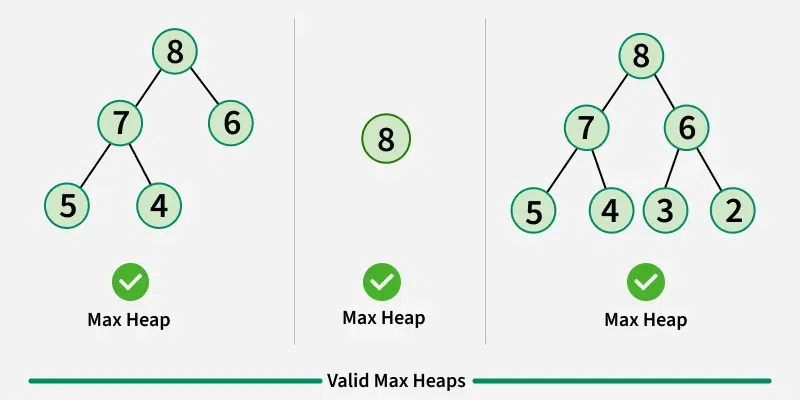
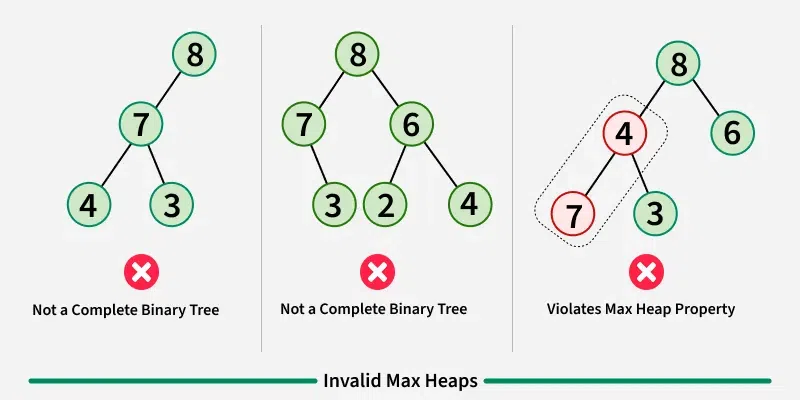
- 最大堆(Max-Heap): 每个节点的值都大于或等于其子节点的值。
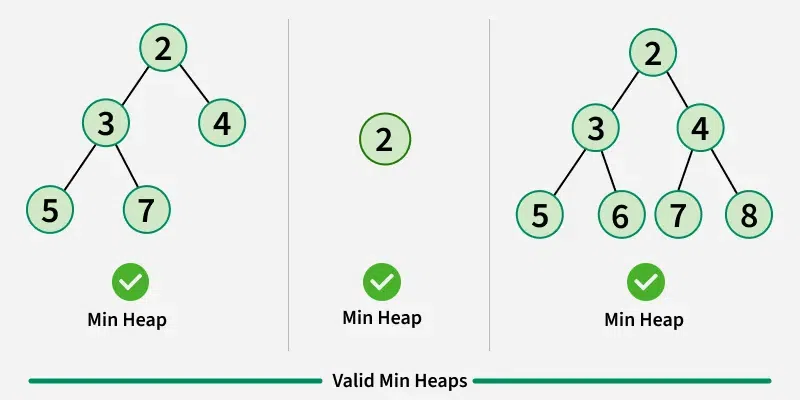
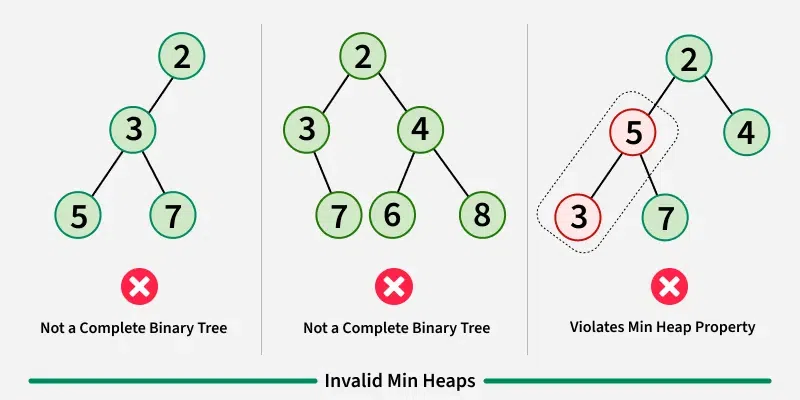
- 最小堆(Min-Heap): 每个节点的值都小于或等于其子节点的值。
堆的性质
- 完全二叉树: 堆一般用数组来实现,可以看作是一棵完全二叉树。
- 堆序性: 堆中每个节点的值都满足堆序性。
堆的应用
堆在计算机科学中有着广泛的应用,主要包括:
- 优先队列: 堆常用于实现优先队列,例如在贪心算法和A*搜索算法中。
- 堆排序: 堆排序是一种高效的排序算法,时间复杂度为O(nlogn)。
- 求第k大/小元素: 利用堆可以高效地求取无序数组中的第k大/小元素。
堆的实现
堆通常用数组来实现,数组的下标从1开始。对于一个节点i,其左子节点的下标为2i,右子节点的下标为2i+1,父节点的下标为i/2。
堆的操作
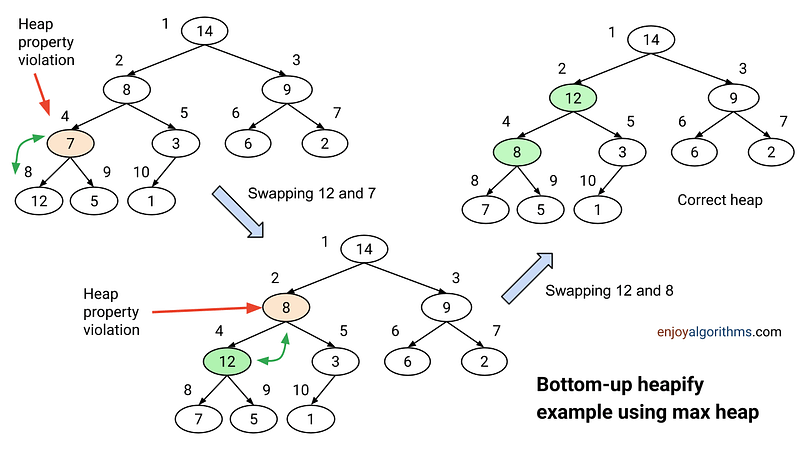
- 插入: 将新元素插入到堆的末尾,然后向上调整(heapify up)直到满足堆序性。
- 删除: 将堆顶元素与最后一个元素交换,然后向下调整(heapify down)直到满足堆序性。
- 查找最小/最大值: 堆顶元素就是最小/最大值。
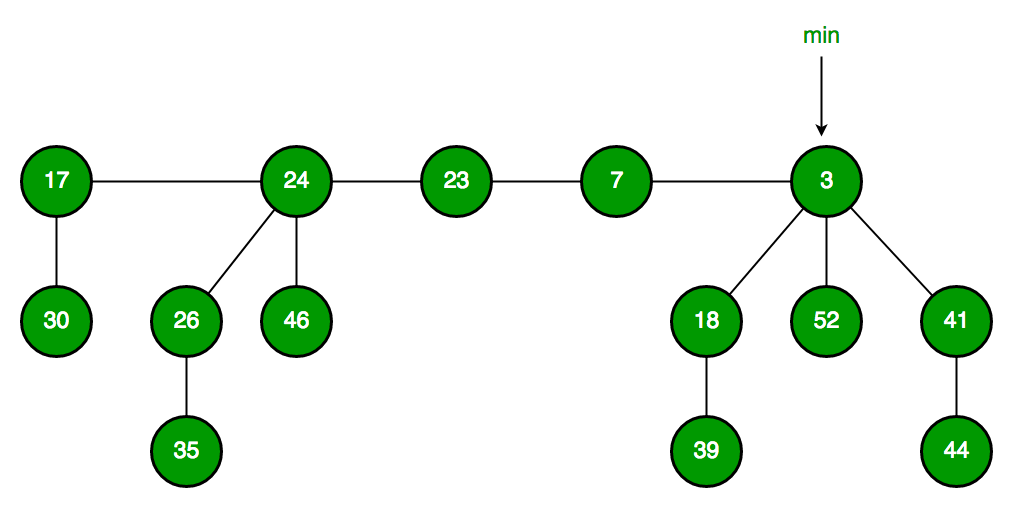
斐波那契堆
斐波那契堆是一种更为复杂但高效的堆数据结构。它在某些操作上具有更好的摊还时间复杂度,如插入、删除最小值等。斐波那契堆由一组最小堆序的有根树组成,每个树的根节点通过双向循环链表连接起来。
堆的代码实现(php)
最小堆(Min-Heap)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
class MinHeap {
private $heap;
public function __construct() {
$this->heap = [];
}
public function insert($value) {
$this->heap[] = $value;
$this->heapifyUp(count($this->heap) - 1);
}
public function extractMin() {
if (empty($this->heap)) {
throw new UnderflowException("Heap is empty");
}
$min = $this->heap[0];
$last = array_pop($this->heap);
if (!empty($this->heap)) {
$this->heap[0] = $last;
$this->heapifyDown(0);
}
return $min;
}
private function heapifyUp($index) {
while ($index > 0) {
$parentIndex = (int)(($index - 1) / 2);
if ($this->heap[$index] >= $this->heap[$parentIndex]) {
break;
}
$this->swap($index, $parentIndex);
$index = $parentIndex;
}
}
private function heapifyDown($index) {
$size = count($this->heap);
while (true) {
$leftChildIndex = 2 * $index + 1;
$rightChildIndex = 2 * $index + 2;
$smallest = $index;
if ($leftChildIndex < $size && $this->heap[$leftChildIndex] < $this->heap[$smallest]) {
$smallest = $leftChildIndex;
}
if ($rightChildIndex < $size && $this->heap[$rightChildIndex] < $this->heap[$smallest]) {
$smallest = $rightChildIndex;
}
if ($smallest === $index) {
break;
}
$this->swap($index, $smallest);
$index = $smallest;
}
}
private function swap($i, $j) {
$temp = $this->heap[$i];
$this->heap[$i] = $this->heap[$j];
$this->heap[$j] = $temp;
}
}
// 示例使用
$minHeap = new MinHeap();
$minHeap->insert(10);
$minHeap->insert(5);
$minHeap->insert(3);
$minHeap->insert(2);
$minHeap->insert(7);
echo $minHeap->extractMin(); // 输出 2
echo $minHeap->extractMin(); // 输出 3最大堆(Max-Heap)
1 |
|
- 解释
类构造:
MinHeap和MaxHeap类都有一个私有数组$heap来存储堆元素。
插入操作:
insert($value)方法将新值添加到堆的末尾,然后调用heapifyUp方法将其上浮到正确位置。
删除操作:
extractMin()和extractMax()方法分别用于提取并删除最小堆中的最小值和最大堆中的最大值。- 通过交换根节点和最后一个节点的值,然后将根节点下沉到正确位置。
堆化操作:
heapifyUp($index)方法用于在插入新元素后将其上浮到正确位置。heapifyDown($index)方法用于在删除根节点后将新的根节点下沉到正确位置。
交换操作:
swap($i, $j)方法用于交换数组中两个元素的位置
总结
堆是一种非常有用的数据结构,在算法设计中有着广泛的应用。通过了解堆的性质、操作和实现,可以更好地解决各种算法问题。








