一、Grover算法概述
Grover算法是由计算机科学家Lov Grover于1996年提出的一种量子搜索算法,它能够在未排序数据库中以$O(\sqrt{N})$的时间复杂度查找特定元素,相比经典算法的$O(N)$搜索时间实现了二次加速。这种算法不依赖问题的特殊结构,具有广泛的适用性,成为量子计算领域最具实用潜力的算法之一。随着量子计算机硬件的发展,Grover算法在密码分析、优化搜索、机器学习等领域展现出颠覆性应用前景。
二、技术原理深度解析
1. 数学基础:振幅放大原理
Grover算法的核心是通过量子叠加态和振幅放大技术,逐步提高目标状态的概率幅:
迭代过程:
- Oracle操作:标记目标状态 $|w\rangle$(相位反转)
- 扩散算子:放大目标状态概率幅
- 重复迭代:约 $\frac{\pi}{4}\sqrt{N/M}$ 次
2. 量子电路设计
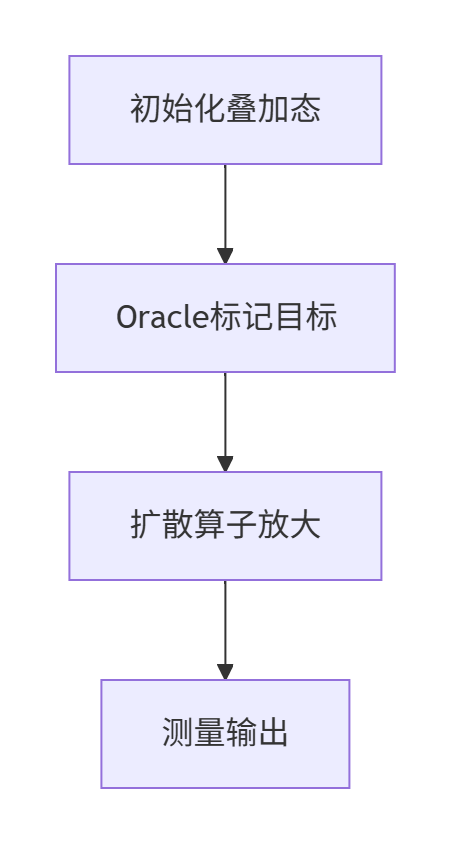
关键组件:
- Oracle:黑箱操作 $U_w|x\rangle = (-1)^{f(x)}|x\rangle$
- 扩散算子:$D = 2|\psi\rangle\langle\psi| - I$
3. 复杂度对比
| 算法类型 |
时间复杂度 |
查询次数 |
| 经典搜索 |
$O(N)$ |
$N$ |
| Grover算法 |
$O(\sqrt{N})$ |
$\sqrt{N}$ |
| 量子行走 |
$O(\sqrt{N\log N})$ |
- |
三、应用场景分析
1. 密码学领域冲击
| 应用场景 |
经典复杂度 |
Grover加速后 |
| 对称密钥搜索(AES-128) |
$2^{128}$ |
$2^{64}$ |
| 密码哈希碰撞 |
$2^{n/2}$ |
$2^{n/4}$ |
| RSA私钥搜索 |
无直接加速 |
需结合其他算法 |
实际影响:
- 对称密钥长度需加倍(AES-128→AES-256)
- 哈希函数安全边际减半
2. 优化搜索问题
(1)图论搜索
(2)数据库查询
3. 机器学习加速
1
2
3
4
5
6
7
8
9
|
def quantum_kmeans(data_points, k):
for point in data_points:
centroids = quantum_oracle(point, k)
amplitudes = grover_amplify(centroids)
nearest_centroid = measure(amplitudes)
update_centroid(nearest_centroid, point)
return centroids
|
四、优缺点对比分析
1. 核心优势
| 特性 |
优势表现 |
| 加速能力 |
查询复杂度降低$\sqrt{N}$倍 |
| 普适性 |
适用于任何搜索问题 |
| 硬件友好 |
仅需基本量子门操作 |
| 可扩展性 |
适用于高维搜索空间 |
2. 现存局限性
| 挑战类型 |
具体问题 |
当前解决方案 |
| 量子硬件 |
需要数百到数千量子比特 |
逻辑量子比特纠错 |
| Oracle实现 |
复杂问题需定制量子电路 |
近似Oracle设计 |
| 误差累积 |
迭代次数多导致误差放大 |
动态误差校正 |
五、代码示例与实验模拟
1. 经典模拟Grover算法(Python)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
| import numpy as np
from math import sqrt, pi, asin
def grover_simulation(N, M=1):
"""经典模拟Grover算法的搜索过程"""
psi = np.ones(N) / sqrt(N)
theta = asin(sqrt(M/N))
iterations = int(round(pi/(4*theta) - 0.5))
def oracle(state):
state[0] *= -1
return state
def diffusion(state):
mean = np.mean(state)
return 2*mean - state
for _ in range(iterations):
psi = oracle(psi.copy())
psi = diffusion(psi)
probabilities = np.abs(psi)**2
return np.argmax(probabilities)
print(grover_simulation(1024))
|
注意:此代码为经典模拟,实际量子实现需用量子电路。
2. Qiskit量子实现框架
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
| from qiskit import QuantumCircuit, Aer, execute
from qiskit.visualization import plot_histogram
def grover_circuit(N, M=1):
"""构建Grover算法的量子电路"""
n = int(np.ceil(np.log2(N)))
qc = QuantumCircuit(n, n)
qc.h(range(n))
theta = np.arcsin(np.sqrt(M/N))
iterations = int(np.round(np.pi/(4*theta) - 0.5))
if N == 4:
qc.cz(0, 1)
qc.h(range(n))
qc.x(range(n))
qc.h(n-1)
qc.mct(list(range(n-1)), n-1)
qc.h(n-1)
qc.x(range(n))
qc.h(range(n))
for _ in range(iterations):
if N == 4:
qc.cz(0, 1)
qc.h(range(n))
qc.x(range(n))
qc.h(n-1)
qc.mct(list(range(n-1)), n-1)
qc.h(n-1)
qc.x(range(n))
qc.h(range(n))
qc.measure(range(n), range(n))
return qc
qc = grover_circuit(4)
backend = Aer.get_backend('qasm_simulator')
result = execute(qc, backend, shots=1000).result()
plot_histogram(result.get_counts())
|
六、未来发展趋势
1. 硬件实现路线图
| 年份 |
技术节点 |
目标规模 |
| 2025 |
100-1000物理量子比特 |
实现小规模Grover |
| 2030 |
逻辑量子比特纠错 |
商用级搜索加速 |
| 2035 |
百万物理量子比特 |
全面密码分析能力 |
2. 新兴应用领域
- 量子机器学习:加速支持向量机训练
- 网络安全:实时入侵检测模式匹配
- 生物信息学:基因序列快速比对
3. 混合计算架构

七、防御策略与应对建议
1. 密码学应对措施
- 对称加密:密钥长度加倍(AES-128→AES-256)
- 哈希函数:增加输出长度(SHA-256→SHA-512)
- 抗量子算法:采用格密码等PQC方案
2. 技术发展路线
1
2
3
4
5
6
7
8
9
10
11
| gantt
title Grover防御升级计划
section 评估阶段
密码体系审计 :20XX, 6m
量子风险评估 :20XX, 3m
section 过渡阶段
密钥长度升级 :20XX, 12m
混合加密部署 :20XX, 18m
section 全面转型
PQC全面替换 :20XX, 24m
量子监控体系 :20XX, 12m
|
Grover算法作为量子计算领域的里程碑式突破,正在重塑搜索问题的解决方案范式。尽管实用化量子计算机仍面临技术挑战,但算法的理论价值和潜在应用已推动学术界和产业界加速布局。理解Grover算法的原理与影响,不仅是技术人员的必修课,更是应对量子时代安全挑战的战略需要。在经典与量子的博弈中,主动创新、提前防御将成为决定技术发展主导权的关键因素。










